( ) It was much later I understood why is that values are a bit out of place.
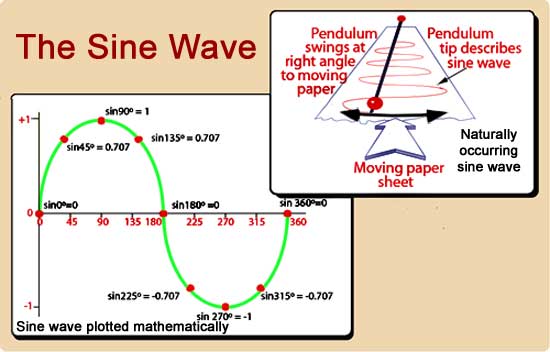
( ) Carefully consider sin (45) .
( ) Sin(45) has a 1/2 in it but with a square-root. Sin (45) = sqrt (1/2).
So now why does this square root come? Good question. Thank you.
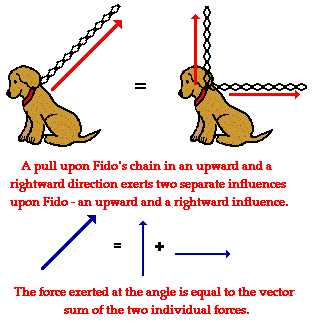
( ) Squares and Square-roots come in Math whenever two forces/events occur simultaneously to produce a net effect.
( ) The two forces or events will be of equal magnitude obviously.
( ) If the two forces produce a net increase.....squares come into the picture.
( ) If they produce a net reduction....then square-roots come into the picture.
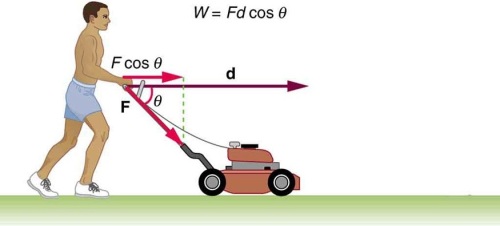
( ) So lets say you tilt a rod which is producing a shadow at a wall. At 90 degrees it was producing full shadow of itself upon the wall.
( ) But now you catch its one end and decide to tilt it to a lower angle say 60 degrees. Now when it tilts to a lesser angle.....both its ends are participating....its upper end moves towards the right say and its lower end moves towards the left say.
( ) These two events are of equal magnitude....and are happening simultaneoulsy and are producing a net reduction in the shadow projected upon the wall. So square roots come into the picture.
( ) Also note if instead of two it were three events contributing to the net decrease....then that is when cube-roots come into the picture. If the three events contribute to the net increase....then only cube.
||||||||||||||||||||||||||||||||||||||||||||||
VISUALIZING MATHS.PDF
AVAILABLE FOR PURCHASE FOR 5$ (INR 300) HERE (PDF)
ABOUT
I hardly understood Math in school. In fact was on the verge of dropping the subject I loved the most because as much as I loved the theory of it, I could not understand the math involved in it. However I loved the subject too much to be able to live without. Hopelessly, I was continuing my love-affair with it.
Then one day....a miracle happened,....while applying a certain formula again and again.....I came to know its significance. Slowly and steadily....other equations also started clicking. I got to see a strong relationship between Maths and the Physics it was pointing towards. They both were the same. Maths was just an easy language to express a physical phenomenon. And a bit more to that in the sense that it could even predict the behaviour of a certain physical phenomenon. Equations now as if came to life.
Every equation now had as if something to say. A burning urge to share these things with the world aflamed within me. So that no one has to give up the subject that he or she loves the most.
Every equation now had as if something to say. A burning urge to share these things with the world aflamed within me. So that no one has to give up the subject that he or she loves the most.
The book on visualizing maths thus got written as a sprout of inspiration. The blog followed. Both these are dedicated to you and all such similar minds searching for answers.
Visualizing Math & Physics is a blog dedicated to you and all such similar minds searching for answers.
||||||||||||||||||||||||||||||||||||||||||||||
CONTACT
binnoypanicker@gmail.com
||||||||||||||||||||||||||||||||||||||||||||||