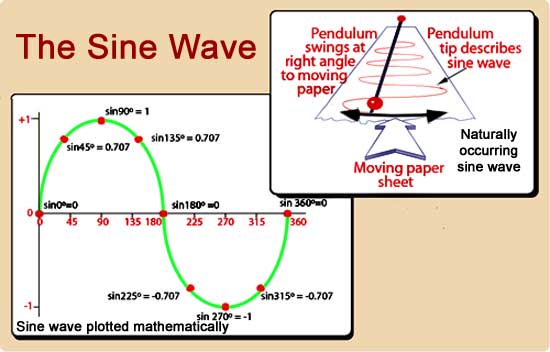
||(/\)||Sine-waves come in mathematics to represent two opposite motions or energies.....the ying and yang the night and day, the up and down so on....||(/\)|| The smoother a sine-wave it....that means the smoother the transition is from up to down or from night to day from summer to winter etc.||(/\)||Infact if you take the example of duration of days every year....that too will form a sine-wave if plotted on a graph.
||(/\)|| The duration of days will keep increasing and increasing smoothly and gradually until it reaches June 21.||(/\)||June 21 if I am not wrong is some Summer Solstice...the longest day of the year. This will form our peak of the sine-wave. ||(/\)|| From June 21st however the length of daytime will keep on reducing smoothly and gradually until it reaches Dec 21st.(Still scared the world will end?)||(/\)||December 21 is the shortest day of the year.This is going to be the bottom peak of our sine-wave.||(/\)|| From December 21st forward on however the length of days will increase and the process will keep repeating.THE WASHING MACHINE ANALOGY|( )|Water in a washing machine moves to and fro in a circular manner.|( )|If you plot this on a graph, what you get is a sine-wave.|( )|Lets say when the water moves towards the right you plot it upwards on the graph.|( )|Initially the water picks up speed in the right direction until it reaches the maximum speed. This is the peak of our sine wave. |( )|Then the water starts losing speed and comes to a halt. This is when you see the gradual descent from the peak. When the water is at halt...that is the zeroth location of the graph.|( )| After halting at the zeroth location...now the water starts moving in the left direction.|( )|It catches speed and until it reaches the peak speed in the left direction. This is the bottom peak of the sine-wave....and then the process repeats.
A.C & Sine-waves.|( )|Electricity called as A.C which is alternating current also moves much similar to water in the washing machine in alternating directions. |( )| Ever wondered why it is called as alternating current? It alternates its direction every now and then. It is more like a churning of electricity through the conductor.
.A.C & Sine-waves.|( )|Electricity called as A.C which is alternating current also moves much similar to water in the washing machine in alternating directions. |( )| Ever wondered why it is called as alternating current? It alternates its direction every now and then. It is more like a churning of electricity through the conductor.
AVAILABLE FOR PURCHASE FOR 5$ (INR 300) HERE (PDF)
ABOUT
Then one day....a miracle happened,....while applying a certain formula again and again.....I came to know its significance. Slowly and steadily....other equations also started clicking. I got to see a strong relationship between Maths and the Physics it was pointing towards. They both were the same. Maths was just an easy language to express a physical phenomenon. And a bit more to that in the sense that it could even predict the behaviour of a certain physical phenomenon. Equations now as if came to life.
Every equation now had as if something to say. A burning urge to share these things with the world aflamed within me. So that no one has to give up the subject that he or she loves the most.
Every equation now had as if something to say. A burning urge to share these things with the world aflamed within me. So that no one has to give up the subject that he or she loves the most.
The book on visualizing maths thus got written as a sprout of inspiration. The blog followed. Both these are dedicated to you and all such similar minds searching for answers.
Visualizing Math & Physics is a blog dedicated to you and all such similar minds searching for answers.
CONTACT
binnoypanicker@gmail.com
SOME COOL LINKS ABOUT SINE WAVES.Amazing animations on sinewaves here.Another page of great animation for sinewaves hereAn intuitive understanding of sinewaves from betterexplained.com here.
giphy.com is famous for gif animation such as..
giphy.com is famous for gif animation such as..
Enjoy giphy.com here.
One interesting link on sine waves here
&
and here
& more on sine waves here
why nature gives much preference to sine wave because all the changes in nature always in the sine wave.
ReplyDeleteHi,
DeleteGanesh Naik.
Your question is valid. Nature doesn't give preference to sine waves.
A cos wave for example is nothing but a sin wave delayed or advanced by 90 degree.
Imagine you have to plot a wave on a graph.
CASE 1
You start plotting such that at the starting point (origin ) of the graph..the wave is at point zero. (AT x=0 ,...y = 0)
At x=0....y=0
i.e maybe at time = 0 sec .....the wave-height = 0.
Such a wave that is at zero point at the beginning of the graph is a sinewave.
Case 2
You start plotting the wave such that at the beginning of the graph i.e at x = 0 or time = 0....the wave is at the highest point i.e at 90 degrees.
So at time = 0 sec....the wave is at y = 90 degrees.
(AT x=0,....y=max = maximum possible height of wave.)
Such a wave is a Cos wave.
So there is no much difference between a sine wave or a cos wave. It just depends upon from where you start plotting.
I hope I interpreted the question properly.
Binnoy.