VECTORS: Significance &Application of Cross product and Dot product.
DOT PRODUCT.
|||| A.B = |A||B|Cos(angle).
EXAMPLE
Haven't you wondered why cos?
|||| Like I said in my post on TRIGONOMETRY, Cos comes into equations when two forces work hand in hand-in-hand with each other to produce the net resultant.
|||| Dot product is also similar. It is used when Two forces A and B produce maximum effect or impact when work together 'in a line'.
|||| A.B = |A||B| Cos(angle) means that the resulting force is due to
1] Force of A
2] Force of B
3] Angle in which A and B are colliding into each other.
|||| Cos in the equation is like telling that, "if you want maximum impact, place A are B as parallel to each other as possible".
|||| For example, if you are rowing a river, row as parallel as possible to the flow of the river to get maximum results.
|||| Multiplication again means combination. Thus A and B and the angle of A and B working together as if are combining to form the net result.
CROSS PRODUCT
|||| Cross-product is a measure of how much perpendicular two objects work in relation to each other.
|||| Cross product comes into picture whenever two objects work against each other, completely out of line and produce maximum impact when perpendicular.
|||| Now imagine the same boat and the same river, but this time instead of measuring the velocity of the river, you want to measure the friction between the boat and the river .
|||| In other words, instead of trying to measure maximum velocity, you want to produce maximum friction between your boat and the river.
|||| Now this will happen when your boat is at 90 degrees to the flow of the river.
|||| Thus maximum friction is when your boat is at cross with the river.
|||| Thus A X B = |A||B| Sin (angle).
|||| Sin as I said comes into those equations where max impact is at perpedicular angles or when two things work against each other or out of alignment.
|||| Thus we can say that Cross-product comes when we have to measure those forces like friction which happen when two objects work against each other and Dot-product comes when we have to measure those forces like total additive velocity which happen when two forces work hand-in-hand with each other.
Hope this helps
BINNOY
||||||||||||||||||||||||||||||||||||||||||||||
THE ABOVE IS A EXCERPT FROM A BOOK AVAILABLE FOR PURCHASE (5$) AT THE FOLLOWING LINK
VISUALIZING MATHS.PDF
CONTACT
binnoypanicker@gmail.com
USEFUL LINKS
A GOOD EXAMPLE OF DOT PRODUCT
ANOTHER EXPLANATION OF DOT PRODUCT
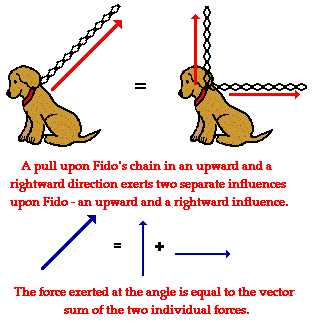
DOT-PRODUCT AND CROSS-PRODUCT LINK FROM PHYSICS CLASSROOMS.COM
DOT PRODUCT EXAMPLE IS GOOD
DOT PRODUCT.
|||| A.B = |A||B|Cos(angle).
EXAMPLE
Haven't you wondered why cos?
|||| Like I said in my post on TRIGONOMETRY, Cos comes into equations when two forces work hand in hand-in-hand with each other to produce the net resultant.
|||| Dot product is also similar. It is used when Two forces A and B produce maximum effect or impact when work together 'in a line'.
|||| A.B = |A||B| Cos(angle) means that the resulting force is due to
1] Force of A
2] Force of B
3] Angle in which A and B are colliding into each other.
|||| Cos in the equation is like telling that, "if you want maximum impact, place A are B as parallel to each other as possible".
|||| For example, if you are rowing a river, row as parallel as possible to the flow of the river to get maximum results.
|||| Multiplication again means combination. Thus A and B and the angle of A and B working together as if are combining to form the net result.
CROSS PRODUCT
|||| Cross-product is a measure of how much perpendicular two objects work in relation to each other.
|||| Cross product comes into picture whenever two objects work against each other, completely out of line and produce maximum impact when perpendicular.
|||| Now imagine the same boat and the same river, but this time instead of measuring the velocity of the river, you want to measure the friction between the boat and the river .
|||| In other words, instead of trying to measure maximum velocity, you want to produce maximum friction between your boat and the river.
|||| Now this will happen when your boat is at 90 degrees to the flow of the river.
|||| Thus maximum friction is when your boat is at cross with the river.
|||| Thus A X B = |A||B| Sin (angle).
|||| Sin as I said comes into those equations where max impact is at perpedicular angles or when two things work against each other or out of alignment.
Hope this helps
BINNOY
||||||||||||||||||||||||||||||||||||||||||||||
VISUALIZING MATHS.PDF
AVAILABLE FOR PURCHASE FOR 5$ (INR 300) HERE (PDF)
ABOUT
I hardly understood Math in school. In fact was on the verge of dropping the subject I loved the most because as much as I loved the theory of it, I could not understand the math involved in it. However I loved the subject too much to be able to live without. Hopelessly, I was continuing my love-affair with it.
Then one day....a miracle happened,....while applying a certain formula again and again.....I came to know its significance. Slowly and steadily....other equations also started clicking. I got to see a strong relationship between Maths and the Physics it was pointing towards. They both were the same. Maths was just an easy language to express a physical phenomenon. And a bit more to that in the sense that it could even predict the behaviour of a certain physical phenomenon. Equations now as if came to life.
Every equation now had as if something to say. A burning urge to share these things with the world aflamed within me. So that no one has to give up the subject that he or she loves the most.
Every equation now had as if something to say. A burning urge to share these things with the world aflamed within me. So that no one has to give up the subject that he or she loves the most.
The book on visualizing maths thus got written as a sprout of inspiration. The blog followed. Both these are dedicated to you and all such similar minds searching for answers.
Visualizing Math & Physics is a blog dedicated to you and all such similar minds searching for answers.
||||||||||||||||||||||||||||||||||||||||||||||
CONTACT
binnoypanicker@gmail.com
||||||||||||||||||||||||||||||||||||||||||||||
A GOOD EXAMPLE OF DOT PRODUCT
ANOTHER EXPLANATION OF DOT PRODUCT

DOT-PRODUCT AND CROSS-PRODUCT LINK FROM PHYSICS CLASSROOMS.COM
DOT PRODUCT EXAMPLE IS GOOD











hello, thank you for embarking on this page. i was beyond frustrated because i am an arts student and do not take physics. However, I have to take math and i could not see the LINK vectors had with anything but this helps! Or at least I see how vectors can be useful in real life. Your passion for the subject is commendable, keep it up!
ReplyDeleteThank you so much for your words.
DeleteBinnoy
Thanks for the article... it is simple yet powerful.... Its wonderful.... Hats off to you binnoy
ReplyDeleteYou are welcome Raghu
ReplyDeleteBinnoy
"Cross product comes into picture whenever two objects work against each other, completely out of line and produce maximum impact when perpendicular".
ReplyDeleteI have some basic doubt...
|||| Now imagine the same boat and the same river, but this time instead of measuring the velocity of the river, you want to measure the friction between the boat and the river
Friction will be maximum when boat goes in opposite to river flow... so it should be 180 degrees right... but how it produces maximum friction when 90 degrees..
might be i misunderstood some simple concept... pls clear my doubt binnoy.. Thanks
Yeah......Good question.
DeleteWell Raghu......just imagine a boat which is square in size....yes square.
or cubical.
Imagine such a cubical boat (from all sides cubical,...no curves nothing), such a boat moving through a river.
The amount of friction will be more than a normally tapered boat right.
Now just see where the friction will occuring....it will be occuring at that front end mainly of this cube which will be facing the water.
This side of the cube where the water will be hitting is responsible for max friction. And this side is 90 degrees w.r.t to the direction at which water hits it.
Now lets say you get frustuated with this huge friction and you decide to cut the front section of the boat such that it gets tapered at 60 degree w.r.t the direction at which water will hit it when the boat start moving.
Because of the 60 degree tapering....the friction will reduce about sqrt(3)/2 times compared to that horribly designed cube of 90 deg at all sides.
If you still want to make your boat more pointed....by cutting and tapering the front portion to say 30 deg....the friction will reduce further to half as compared to when your boat was a cube having 90 degree edges..
But still why does this happen? Why doesnt the friction dissapear.
It is because no matter how much steeply we curve the boat....there will be parts of it which will have to hit against the water.,,,,especially the front section of the boat.
The more you make the front section perpendicular w.r.t the direction in which you are moving....more the friction.
The more you make this front section tapering.....the lesser the friction.
That is why they make jet planes and concorde and all having peak like front portions.
If you make the front section of the boat infinitely thin....like a thin sheet...and then move it parallel to the flow of the river....its front portion is so thin....it will hardly hit water....
So friction might be around nill....but not nill because this sheet still will have some thickness to it,
So friction in case of a boat will come into play due to water hitting some section of your boat which lies somewhat perpendicular to the direction in which water will be hitting it .
NOW WHY IS THAT AT IF YOU MOVE AT 180 DEGREES WITH RESPECT TO THE RIVER.....FRICTION WILL INCREASE..
Well consider...two cases...
case 1
You move in the same direction of the river....in this case....the water particles in the river and your boat , they are moving in the same direction....so the water particles will hit the front of your boat less vigirously. So you will feel the fury of these water particles less and so less friction.
Case 2
If you move in the opposite direction of the river.....the relative velocity between you and the water particles will be very high.
Now not only will the water particles hit you more vigirously
....but your boat also with its own velocity will hit the water in the river more vigirously..
Its like if you collide into a person who was running in the opposite direction in which you were running....wont the impact be higher..
On the other hand if you collide into a person who was running in the same direction in which you were running but somewhat slow....wont the impact be lower??
So The fricition will be depending on two things..
1] How perpendicular the front section is w.r.t to the flow of water...(so a cross product here)
2] How aligned you are with the flow of water...(so dot-product here).
So the equation of friction will have i think cross-product and dot-product together.
So it will have sin( ) and cos ( ) both in its equation.
A great question by the way!!!
Let me know if there are any further questions.
Hope this helps
Binnoy
in case of electromagnetic wave ,why there considering the sin(angle)?
ReplyDeleteHi,
DeleteIts a brilliant question that 'IN CASE OF ELECTROMAGNETIC WAVE,...WHY ARE THEY CONSIDERING THE SIN(ANGLE)?
To understand this.....just draw an electromagnetic wave on a paper.
Now after it is drawn....move a pencil along its borders.
What is noticed?
1) The angle at which you have to move your hand changes as you move along varies( angle varies).
2) You find the angles or patterns repeating themselves after regular intervals (periodic motion).
So lets say you are plotting this sin wave now on a graph.
You just have to do y = sin (x).
If you want some quantities instead of x and y.....just say time on x-axis and height of wave on y-axis....
then you can say that HEIGHT = sin (TIME)
When time = 0 sec...height = sin(time) = sin(0) =0
When time = 90millisecons......height=sin(time) = sin(90) = 1.
When time = 180milliseconds...height = sin (time) = sin(180) =0
When time = 270milliseconds...height = sin(time) = sin(270) = 1.
Now sin, i said is a measure of how much out of alignement one thing is with other.
So just observe a sin wave....At 90 degrees...the wave is out of alignment w.r.t the y-axis and at 0 degrees...the wave is fully in alignment w.r.t the y-axis.
Just draw a tangent to the wave when it is at 0 on the x-axis.....you will see the tangent is parallel to the y-axis....thus at x=0 the wave is 0% perpendicular to the y-axis ....hence sin(0) = 0.
Just draw now a tangent to the wave when it is at 90 milliseconds....i.e at x = 90 milliseconds.
This tangent will be fully perpendicular ( fully out of alignment ) w.r.t the y-axis.
And since sin( ) is a measure of how much perpendicular or out of alignment two forces are .......sin (90) = max = maximum height of the wave.
Hope this helps
Binnoy
can u give some more real life example of cross product
ReplyDeleteI have one suggestion. Please check background color.
ReplyDeletelevel
ReplyDeleteI learned cross and dot products just today, and my goodness! The inaccuracies here are shocking! You have repeatedly confused vector addition with vector multiplication. The "sideway" force should not be the dot product of the boat force and river force, it will be the sum of these two forces. The dog leash example pertains to vector addition and has nothing to do with dot product. As for the cross product example, I have no idea what you mean the boat being perpendicular to the river flow. What part of the boat? The bottom of the boat (that accounts for the friction) is somewhat parallel to the river flow and not perpendicular to it. Frictional force is indeed maximum on a flat surface because frictional force is perpendicular to weight force. However, this has nothing to do with cross product. Frictional force is not a cross product but a scalar multiple of normal force. As frequently the example you have given in your comment, boats and jets have their shape to reduce surface friction (this has nothing to do with "angles" and more to do with how much surface is in contact with water/air) and because of "form drag" or how well the boat/jet divides water/air. When you say the cross product applies when two objects work against each other I suppose you mean two vectors. "Work against each other can be misleading". Two vectors in opposite directions (which could be seen to work against each other) will have a smaller cross product magnitude than two vectors (of the same magnitude) which are perpendicular. When you say the dot product refers to how parallel two vectors are and cross product refers to how perpendicular two vectors are you might as well refer to the angle between the two vectors, because you make no mention of the vectors' magnitudes. A better way to explain dot product might be that it is the product of one vector and the component of the other vector in it's same direction, while a cross product is the the product of one vector and the component of the other vector that is not in it's direction. I just started reading about vectors yesterday and I don't believe I am saying this to a person who has written a book on this matter!
ReplyDeleteHi, thanks for the great article. According to your explanation, why is the direction of the cross product in the third dimension? It doesn't make so much sense with the river - boat analogy
ReplyDeleteAmazing Sir !!
ReplyDeleteThis content is simply exciting and creative. I have been deciding on a institutional move and this has helped me with one aspect. Mercruiser Alpha One outdrive replacement
ReplyDeletethe significance and application of vector is explained in a clear manner pls update more information about its type
ReplyDeleteCBSE schools in Vellore
the blog is very unique and is easy to understand
ReplyDeleteSchools in Vellore
Cool and I have a super offer: House Renovation What To Do First house renovation mortgage
ReplyDelete