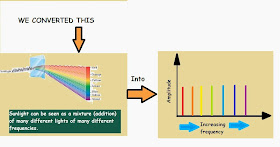
|||| Now each color of light has a distinct frequency, isnt it?
|||| Now, lets say we want to arrange these colors in increasing order of their frequencies.
|||| It will look like this.,......below.
|||| Now lets see what we did around here,
|||| Now, lets take just one of them,...hmmmm.. RED for example.
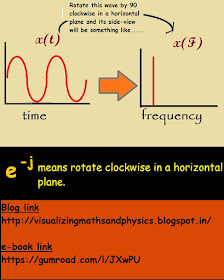
|||| x(t) is the waveform which is a function of time.
|||| When this waveform i.e x(t) is rotated in a horizontal plane......
YES....
e^j---------> Rotation in the anticlockwise direction in a horizontal plane.
e^-j---------> Rotation in the clockwise direction in a horizontal plane.
(By the way....e^i --------> Rotation in the vertical plane.)
|||| Now e^ j(2.pie.freq.time) = cos(2.pie.freq.time) + j.sin(2.pie.freq.time)
Where....cos(2.pie.freq.time) = Horizontal component of the waveform.
and... sin(2.pie.freq.time) = Vertical component of the waveform.
|||| So now,.....if you are removing the horizontal as well as the vertical component component from a wave what remains?
|||| Well....lets see. Every wave can be expressed in the form A.e^(j0) . Now if you remove e^(i0) by dividing it by itself what remains? Only A right and A is the amplitude of the wave.
|||| So basically, when you divide a waveform by all its horizontal and vertical components,...you are always and always left only with its amplitude.
|||| This amplitude is what you plot in the frequency spectrum. You plot the amplitude at that point on the X-axis which co-incides with the frequency of the wave.
|||| Now lets say you want to plot the entire vibgyor on the frequency spectrum. So now for that you will have to keep on adding all the amplitudes of all the different colors onto the frequency spectrum graph.
|||| Integration is another term for adding.
|||| So,... Integration of (e^(2.pie.freq.time)) = adding all the amplitudes of all of colors (from Red to violet) one after the other(This is synonymus to plotting them on a graph one after the other).
|||| So basically if there was an algorithm for fourier transforms....it would be as follows.....
Another way of putting it .......
ALTERNATE USEFUL EXPLANATION THROUGH WIKIPEDIA IMAGE
NOW WHAT IS THE APPLICATION OF FOURIER TRANSFORMS???????
|||| Truth being told, I myself dont know it fully.
|||| The below image from wikipedia is the best explanation I could get.
BUY
AVAILABLE FOR PURCHASE FOR 5$ (INR 300) HERE (PDF)
ABOUT
I hardly understood Math in school. In fact was on the verge of dropping the subject I loved the most because as much as I loved the theory of it, I could not understand the math involved in it. However I loved the subject too much to be able to live without. Hopelessly, I was continuing my love-affair with it.
Then one day....a miracle happened,....while applying a certain formula again and again.....I came to know its significance. Slowly and steadily....other equations also started clicking. I got to see a strong relationship between Maths and the Physics it was pointing towards. They both were the same. Maths was just an easy language to express a physical phenomenon. And a bit more to that in the sense that it could even predict the behaviour of a certain physical phenomenon. Equations now as if came to life.
Every equation now had as if something to say. A burning urge to share these things with the world aflamed within me. So that no one has to give up the subject that he or she loves the most.
Every equation now had as if something to say. A burning urge to share these things with the world aflamed within me. So that no one has to give up the subject that he or she loves the most.
The book on visualizing maths thus got written as a sprout of inspiration. The blog followed. Both these are dedicated to you and all such similar minds searching for answers.
Visualizing Math & Physics is a blog dedicated to you and all such similar minds searching for answers.
CONTACT
binnoypanicker@gmail.com











Truly amazing work. I only wish my teachers had this much understanding on the topic
ReplyDeletesir when i was read this concept, i have some clarity. but when i was watching this video
ReplyDelete:www.youtube.com/watch?v=spUNpyF58BY&t=344s:
i get confused,i can't under stand how he relate it center of mass....please explain.
my email:yshiridibabu@gmail.com
Hi,
ReplyDeleteFirst google image search for "VENN DIAGRAM FOR RGB".
Now the fourier transforms deals with frequencies. Colors that we see are nothing but waves of different frequency.
Now take a color pallete. Mix red, blue and yellow in equal proportions... the center of mass will come to white.
Now pour more of red into the mixture. The center of mass will shift towards red (lower frequency).
Now pour more and more of blue into the mixture. Do this till the mixture turns blue. Now the center of mass has shifted towards the higher frequency.
The center of mass is just an indicator of which frequency component has got more strength in it.
Maybe this video on my channel will help
https://www.youtube.com/watch?v=fmZDlrXuIGw
Hope this helps
Binnoy.